Categories: Astrophysik
Tags: Allgemeine Relativitätstheorie Antigravitation Dr. Klaus Retzlaff klassischer Elektronenradius Reissner-Nordström-Metrik
versendet von: Klaus Retzlaff
Kommentare:4
Antigravitation im klassischen Grenzfall der Reissner-Nordström-Metrik der Allgemeinen Relativitätstheorie
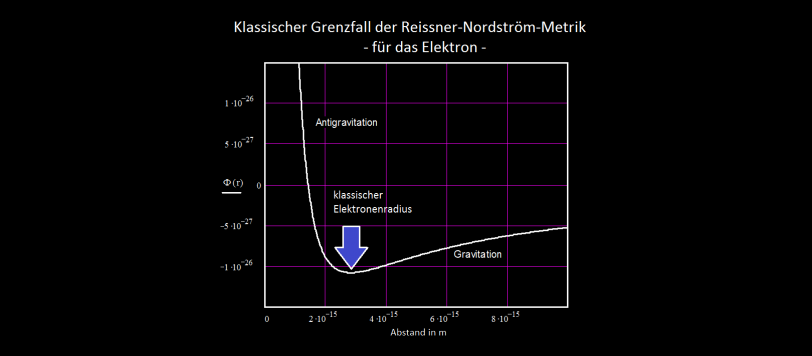
Zusammenfassung: Die Reissner-Nordström-Metrik ist eine exakte, eindeutige, kugelsymmetrische und statische Lösung der Allgemeinen Relativitätstheorie Einsteins (1915). Sie beschreibt die Raum-Zeit um ein elektrisch geladenes Gravitationszentrum. Wir leiten in diesem Artikel den klassischen Grenzfall her, um ihn für weitere Untersuchungen benutzen zu können. Bemerkenswert erscheint die Tatsache, dass der Radius, bei welchem die Dominanz der repulsiven Antigravitation mit der attraktiven Gravitation wechselt (Regimechange), mit dem klassischen Elektronenradius identisch ist.
Title: Antigravity in the classical limit of the Reissner-Nordström metric of general relativity
Abstract: The Reissner-Nordström metric is an exact, unambiguous, spherically symmetric and static solution of the general relativity theory of Einstein (1915). It describes space-time around an electrically charged center of gravity. In this article, we derive the classic borderline case in order to use it for further investigation. Noteworthy is the fact that the radius at which the dominance of repulsive antigravity changes with attractive gravity (regime change) is identical to the classical electron radius.
Images: classical gravitational potential, classic borderline case of the Reissner-Nordström metric (ART), see article, (c) Klaus Retzlaff
Bild: klassisches Gravitationspotential, klassischer Grenzfall der Reissner-Nordström-Metrik (ART), siehe Artikel, (c) Klaus Retzlaff






4 comments
Hallo Herr Andre, Hallo Herr Retzlaff, wie gross ist Ihre ermittelte Überlichtgeschwindigkeit ? mfg M. Kant
Guten Tag Herr Retzlaff,
vor wenigen Tagen las ich diesen Artikel und war danach ganz elektrisiert. Das betrifft vor
allem das Ergebnis, daß hier der klassische Elektronenradius eine Rolle spielt. Ihre
Annahme dabei war, daß das Elektron keinen Drehimpuls besitze (Reissner-Nordström-
Metrik). In der Quantenmechanik wird dem Elektron aber ein Spin ½ zu geschrieben. Sollte
man dann nicht ein rotierendes Elektron annehmen, und die Rechnung hätte mit der Kerr-
Newman-Metrik durchgeführt werden sollen? Vielleicht haben Sie es ja in der Zwischenzeit
schon gemacht. Wenn ja, sind die Ergebnisse mit kleinen Korrekturen gleich oder gibt es
gravierende Unterschiede?
Ihr Artikel ist, was man nicht oft antrifft, durchweg verständlich geschrieben, obwohl einige
Wissensvoraussetzungen erforderlich sind.
Dr.-Ing. Ernst-Christian André, Remseck a.N.
Sehr geehrter Herr Remseck,
in der Tat, könnte man, um eine Rotation einzubeziehen an die Newman-Kerr-Metrik denken. Das war nicht mein Ziel, da ich selbt erst einmal nur über den quantitative Koinzidenz erstaunt war und nie etwas darüber gelesen hatte. Inwiefern die Kerr-Newman-Matrik da noch etwas modifiziert ist vielleicht interessant. Leider überhäufen mich augenblicklich andere Aufgaben.
Mit freundlichen Grüßen,
Dr. Klaus Retzlaff
Guten Tag Herr Retzlaff
Vielen Dank für Ihre Antwort. Wenige Tage, nachdem ich den Kommentar geschrieben habe, hatte ich wegen einer Antwort nachgeschaut. Leider habe ich meinen Kommentar nicht mehr wiedergefunden. Das war wohl mein Fehler. Nun bin ich aber froh, daß ich
gestern auf Ihre Antwort , die schon ein paar Tage zurück liegt, gestoßen bin.
Deshalb möchte ich Ihnen heute mitteilen, warum ich Ihr Ergebnis – Antigravitation im
Bereich unterhalb des klassischen Elektronenradius – so interessant finde.
Ich habe, um Ihren Sprachgebrauch zu benutzen, ebenfalls ein mathematisches Konstrukt
gefunden. In physikalisch unorthodoxer Weise habe ich aus der elektrischen und der
magnetischen Feldkonstanten zwei Urgeschwindigkeiten heraus präpariert, die ich hier mit
v_e und v_m nach ihrer Herkunft bezeichnen möchte. Eigenartigerweise entspricht der halbe
Wert von v_e der Umlaufgeschwindigkeit v_b des Elektrons auf der Bohrschen Bahn im
Wasserstoffatom. Der doppelte Wert von v_m entspricht dann der Rotationsgeschwindigkeit
v_k eines Elektrons mit dem klassischen Elektronenradius (um seine Achse).
In der Folge ergibt sich zum einen die Lichtgeschwindigkeit c als geometrisches Mittel aus
v_b und v_k sowie die Sommerfeldsche Feinstrukturkonstante alpha als Wurzel aus dem
Quotienten v_k / v_b. Wegen dem geometrischen Mittel ist v_b kleiner als c und v_k größer
als c, was es nach Einstein nicht geben sollte.
Nähere Ausführungen habe ich auf meiner Internetseite sonate-x.de in den Paragraphen 1
bis 8 und EE gemacht.
Bliebe zu klären, ob die o.g. Überlichtgeschwindigkeit v_k mit der von Ihnen gefundenen
Antigravitation zu tun hat und ob Ihr und mein Konstrukt irgendwie zusammenhängen und
in der Zukunft doch eine reale Bedeutung erlangen können.
Mit freundlichen Grüßen
Ernst-Christian André